The basics of analyzer sample systems
by Ian Verhappen
If you had to design and install a process analyzer system today, how would you do it? First, remember that an analyzer system is comprised of the sample tap, the sample system, the analyzer, the sample return, the signal transmission, and the control system. If any component of this system fails, your company is not gaining the economic benefits for which the system was installed in the first place. And, don't forget, it is generally accepted that analyzer sample systems are the victims of the Pareto principle (i.e., 20% of a system consumes 80% of the resources) since they are responsible for 80% of analyzer system problems.
As with most things, process analyzer sample systems follow the engineer's "golden rule" (KISS). This time, however, KISS does not mean "Keep It Simple Silly;" instead, it represents a series of guide words to use when installing an analyzer system. The "new" meanings are:
K - Know your process conditions
I - Involve the right people
S - Simplify the system
S - Select the right equipment.
KNOW the Process Conditions
It is important to understand the process conditions not only at the sample inlet but also at the analyzer itself and all along the sample loop. To do this, three basic calculations must be made:
- Dead spaces
- System lag time
- System pressure drop.
Using this information, a phase diagram similar to the one shown in Figure 1 should be generated for all sample streams. This diagram represents how the fraction of liquids, solids, and vapors change as a function of pressure and temperature. It is invaluable when trying to determine if there are condensable products in the stream that an later be vaporized as the pressure decreases. This is similar to checking for cavitation in control valve sizing, only in reverse, since rather than looking for vapor in a liquid one is looking for a momentary liquid phase in a vapor stream. A process or chemical engineer will be able to generate this diagram for you from the stream composition along with a range of pressures and temperatures over which the system may be operating.
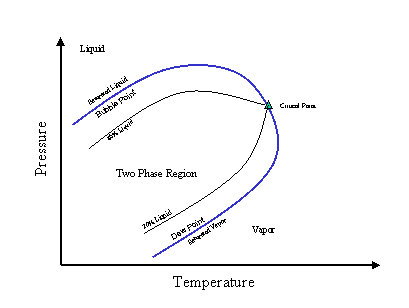
Figure 1. Example of a phase diagram.
Dead spaces are often overlooked
One of the largest and often overlooked items when designing a sample system is dead spaces or volumes. Dead spaces are those parts of the sample system in which pockets of fluid can become trapped and cannot move along with the remainder of the sample as it progresses through the sample system. Perfect places for dead volumes are tee fittings, separators, or any other sharp edged flow change. The flow profile at a tee is shown in Figure 2. A series of eddies form just at the edge of the fitting and fluid becomes trapped in this area, just like a piece of wood behind a rock protruding into a stream. Remember watching sticks float in a ditch or stream and seeing them get stuck behind a rock where they would spin seemingly forever? The same thing happens inside your fittings. To minimize its effect, use the following rules of thumb:
- Minimize the number of tee fittings in the system
- Purge the sample system three times for each analyzer cycle
- Use the smallest size fittings you can to get the job done within other constraints
- Use the minimum number of fittings possible, which not only reduces dead time, it also minimizes the number of potential leak or failure points
- Operate your continuous sample systems in the turbulent flow regime.
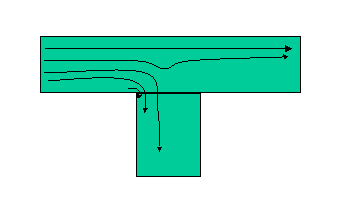
Figure 2. Tee fitting flow (approximate).
A configuration designed to minimize dead volume is shown in Figure 3. The three-way valves eliminate elbows and, when a stream is not flowing to the analyzer for measurement, it is still flowing to a vent or sample return point, ensuring a continuously fresh sample at every point in the system. Figures 4 and 5 show the configuration when streams AX-1A and AX-1B are being analyzed, respectively.
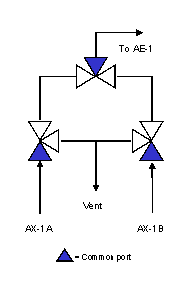
Figure 3. Configuration designed to minimize dead volume.
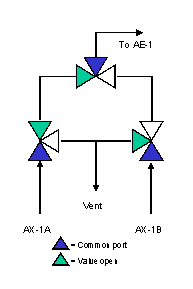
Figure 4. Configuration designed to minimize dead volume - AX-1A on analysis.
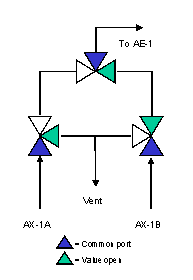
Figure 5. Configuration designed to minimize dead volume - AX-1B on analysis.
System lag time depends on velocity and volume
The second item to consider, and one of the first things to calculate, is the system lag time. System lag time is the sum of the analyzer cycle/measurement time and the sample lag time.
Sample lag time is the amount of time it takes for the sample to travel from the sample point to the analyzer sensor. It is simply the volume of the sample system divided by the velocity of the flow and can be calculated using Equation 1.
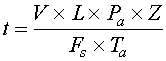
Equation 1
Where:
t = time
V = sample system volume
L = distance from the sample point to the analyzer sensor
Pa = absolute pressure
Z = compressibility factor
Fs = flow rate under standard conditions
Ta = absolute temperature
Compressibility a factor for gases at higher system pressures
For liquids, compressibility is negligible and the compressibility factor (Z) = 1.0. In gas systems operating at more than about 35 to 50 psia, compressibility must be considered. For gases, compressibility changes as a function of pressure and temperature according to the rules of the ideal gas law, as shown in Equation 2.
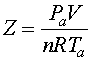
Equation 2
Where:
Z = compressibility factor
Pa = absolute pressure
V= volume
n = moles of fluid
R = gas constant
Ta = absolute temperature
The compressibility factory (Z) can be determined from compressibility charts and the associated reduced temperature (Tr) and reduced pressure (Pr). The reduced temperature and pressure are calculated as follows:
Tr = Ta/Tc
Pr = Pa/Pc
Where:
Tc = y1Tc1 + y2Tc2 + y3Tc3 . . . (yx is the mole fraction and Tcx is the critical temperature of component x)
Pc = y1Pc1 + y2Pc2 + y3Pc3 . . . (yx is the mole fraction and Pcx is the critical pressure of component x)
Don't forget that the ideal gas law uses absolute pressures (Pa) and temperatures (Ta) so calculations must be done in psia or kPa(abs) and degree Rankine (R = F + 460) or degrees Kelvin (K = C + 273.15). By combining and rearranging Equation 2 at two conditions (neglecting n which remains constant), it is possible to estimate the effect of pressure or temperature on volume.
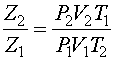
Equation 2a
Thus,
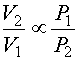
Equation 2b
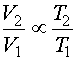
Equation 2c
Where subscript 1 refers to the inlet condition and subscript 2 refers to the outlet condition.
Calculate sample flow
If you have a certain size and length of line and want to figure out an appropriate sample flow rate (Fs), at standard conditions, rearrange Equation 1 as shown in Equation 3
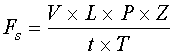
Equation 3
Once you know the volumetric sample flow rate (Fs in liters/min), you can determine the velocity (v in ft/sec) of a stream using Equation 4.
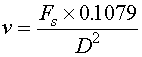
Equation 4
Where:
Fs = volumetric sample flow rate (liters/min)
0.1079 = a conversion factor to get the final result into ft/sec
D = internal pipe diameter (inches).
As a general rule of thumb, the sample system velocity should be in the range of 1-2 m/s (3-6 ft/sec) to insure that any components in the sample are carried along with the sample proper and do not drop out of solution.
System pressure drop depends on velocity
The pressure drop in the system can be calculated using the sample system velocity calculated in Equation 4. This is not as difficult as it sounds although it is important. Often the hardest part of the exercise is getting an estimate of the stream properties.
The equation for pressure drop per 100 feet of tubing is shown in Equation 5.
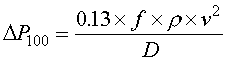
Equation 5
Where:
∆P100 = pressure drop per 100 feet of tubing (psi)
fd = Darcy Friction Factor
ρ = density (lb/ft3)
v = velocity (ft/s)
D = pipe diameter (inches)
To calculate the Darcy friction factor (fd) we need to calculate the Reynold's number, as shown in Equation 6.
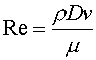
Equation 6
Where:
Re = Reynolds number
ρ = density
v = velocity
μ = viscosity
If the Reynolds number is less than 4,000, the Darcy friction factor is calculated as shown in Equation 7
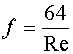
Equation 7
If the Reynolds number is greater than 4,000, the non-iterative equation of A.K. Jaini can be used, as shown in Equation 8.
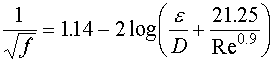
Equation 8
Where:
f = Darcy friction factor
ε = absolute roughness in inches
D = diameter of the pipe in inches
Re = Reynolds number
The Moody friction factor, also known as the Fanning friction factor, is one quarter (+) the Darcy friction factor calculated in Equation 7 or Equation 8. Make sure you know which friction factor you are using and, if needed, adjust accordingly.
The last step in the pressure drop calculation is to determine the equivalent length of pipe. The equivalent length (Le) is a parameter used to represent the total length of pipe of a single diameter that would be equivalent to the actual pipe with all its fittings and line size changes. Crane Technical Paper 410-C is the standard that is used to obtain these parameters.
Crane Technical Paper 410-C uses the concept of 'Equivalent Length' to assign a factor to each type of fitting or change in pipe diameter to a length of straight pipe that would equate to the same pressure drop as the fitting. Each type of pipe change is assigned a 'K' factor as a function of a nominal Friction factor ft. The Crane factor ft is a function of nominal pipe size. The equivalent length factor 'K' in the Crane manual is empirical determined from experimental data. After the 'K' factors have been determined for all the fittings, they are summed and this total equivalent length is then added to the actual pipe run length to calculate a total equivalent length. For example a +-inch pipe system with two 90° elbows and plug valve, the calculation would be as follows:
ft = 0.027 (from the Crane Manual)
Plug valve: K = 18 ft (from the Crane Manual)
Elbow: K = 30 ft (from the Crane Manual)
Therefore Le = (1 x 18 x 0.027) + (2 x 30 x 0.027) = 2.1 feet.
Using this total equivalent length, the system pressure drop can be calculated. Since this exercise is performed so often, two spreadsheets have been developed to calculate a simple pressure drop using Equations 6, 7, and 8. Spreadsheet A is for calculating the pressure drop in a vapor line. Spreadsheet B is for calculating the pressure drop in a liquid line.
The last two "Rules of thumb" for pressure drop calculations are:
- If the calculated pressure drop is greater than one third of the total pressure (i.e. inlet pressure divided by three) the calculation should be done in shorter segments so the outlet pressure of the segment is greater than one third the inlet pressure of that segment.
- Elevation differences between the inlet and outlet of the sample system must be taken into account for liquid streams (the affect on vapor streams will be negligible). Remember, it takes 675 psi to move a column of water up a 25 foot pipe rack. Conversely, and more likely, a water stream gains 675 psi on its way down from the same pipe rack. This could make a difference in how you set your pressure relief valves. The equation to be used is:
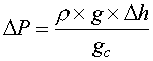
Equation 9
Where:
∆P = pressure drop (feet of liquid or meters of liquid)
ρ = density (lb/ft3 or kg/m3)
h = height (feet or meters)
g = local acceleration due to gravity (ft/sec or m/sec)
gc = gravity constant (32.17 ft/sec or 9.814 m/sec)
Involve the right people
In addition to process engineers, a project team will involve several other people as well. A likely group will include the following:
- Chemist - A representative from the laboratory who will not only provide the stream composition but also know the present method of analysis used on the stream. The team may decide not to use the same method but at least they will know how the methods differ and, therefore, understand why the "answers" may differ as well.
- Maintenance/Analyzer Technician - A person, or group of people, who must be involved from the beginning not only to gain get a sense of ownership of the process but also to understand the technology and equipment before it arrives on-site to get commissioned. This person will also have good ideas on how to arrange the sample system for ongoing maintenance after the unit is operating. After all, it is their knuckles that will get scraped against all those tube fittings.
- Project Manager - A person who coordinates the entire project, gets the funding, arranges for necessary approvals, and other important duties as they come up. It is best if someone familiar with all the steps it takes to complete a project is able to do this so that the designers can concentrate on designing the best system possible within the available budget.
Simplify the sample system
The easiest way to simplify the sample system is to ensure that only the sample you need is being collected. Start with the sample tap itself. Taps can be designed one of the following three ways and should ideally be installed on vertical pipe runs:
- Continuous - The most common sample system where a representative continuous slipstream of the process fluid is withdrawn and transported to the analyzer. To be representative, experience has shown that the sample probe must extend into the center third of the process pipe. Many types of sample probes are available, including blunt pipes, probes with beveled ends (most common), double walled pipes with heating and cooling, as well as automated blow back, dilution, and calibration system connections.
- IsoKinetic - An isokinetic probe is designed to remove a sample from the stream at the same level of kinetic energy (normally represented as velocity) as the process stream itself. This type of probe is typically used in a multiphase stream to insure that all components in the stream are sampled.
- Discrete - In very difficult streams (e.g., extremely hazardous, corrosive, or dirty streams) the most reliable system may be a discrete sampling system in which only a small aliquot of the process fluid is transferred as a plug from the sample tap to the analyzer. The discrete sample is taken at the probe using either an automated sampler or a multiport valve and cylinder or solenoid to introduce a small amount of process material into a continuous flowing inert carrier stream.
Minimize the dead volume by designing the system so there is always a continuous flow in all lines by selective use of three way sampling valves. If the stream is not being routed to the analyzer, route it to either a vent or a recovery system. This also results in a lower lag time. Another way to avoid the problem of dead volume is to insure that the sample system is swept through three times per analysis cycle. This compounds another common problem with sample systems because the analyzer only requires a very low flow rate. Thus, a fast loop is often used, as shown in Figure 6. A fast loop is an external loop with minimal sample conditioning that is cycled to a close proximity to the analyzer and from which the actual sample to the analyzer is taken. A common way to separate the secondary (slow) loop from the primary or fast loop is to flow the sample through a bypass filter. The stream that passes through the filter is the slow or analyzed loop. The fast loop remains unfiltered and also removes any excess material that is trapped or coalesced on the filter.
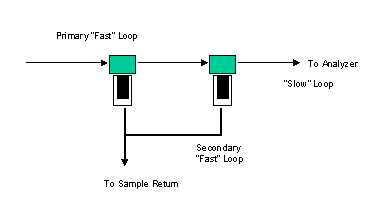
Figure 6. Example of a fast loop - an external loop with minimal sample conditioning that is cycled to a close proximity to the analyzer and from which the actual sample to the analyzer is taken.
Another important consideration is material compatibility, not only to the process fluid but also to the ambient atmosphere and plant conditions. Most designers are very aware of the process compatibility and normally specify 316SS as their tubing material, going with more exotic materials only when required. However, 316SS is not a good choice where it can be exposed to seawater. The chlorine in seawater will cause the metal to fail in a short period of time. Another choice, Tygon tubing, should not be used if it could be exposed to sunlight. After exposure to the ultraviolet light in sunshine for 3 to 4 years, the tubing becomes brittle and fails.
The only remaining problem is how to move all this material around the sample system. This is ideally done through judicious selection of the sample source and return points. If at all possible, two process points of sufficient differential pressure drop should be selected so that no prime mover is required in the sample system. If a prime mover is required, the normal choices are either a centrifugal pump, a positive displacement pump, or an eductor.
If a positive displacement pump is used, be aware that it tends to require more maintenance than a centrifugal pump because it has more moving parts and will likely introduce a pulsating flow to the system. A positive displacement pump also has advantages: it is a constant volume device and typically has a much higher differential pressure output.
If an eductor is used, be sure to check the phase diagram to insure that the process liquid does not enter the eductor at less than 25°F above the bubble point. If it does, experience has shown that there is sufficient pressure drop in the eductor throat to cause the fluid to vaporize (cavitation) and as a result most of the energy introduced to the eductor to induce flow in the secondary stream will be lost.
Select the right analyzer
After doing all the calculations to ensure that your analyzer system will operate properly, it is vital that the sample system be linked to the analyzer itself. In most cases, the analyzer selected will dictate to some degree the type and size of sample system installed. However, if the analyzer is not suitable or able to detect the components of interest in the general surrounding process stream all is for naught.
The three R's of analyzer selection:
- Reliability - The analyzer must be highly reliable so it will maintain a service factor in excess of 95%.
- Repeatability - The output of the equipment must be repeatable for a given input. It need not be accurate (though of course this is desirable) but it must always give the same numeric output for a given calibration or process sample.
- Return - Every analyzer system installation must have an economic return or justification. If it is not used for some form of continuous monitoring or control the unit will not get the attention it receives to remain in operation at the required service factors to be considered reliable.
Additional Information
- Spreadsheet for calculating the pressure drop in a liquid line.
- Spreadsheet for calculating the pressure drop in a vapor line.
For Further Reading
Jain, A.K. 1976. Accurate Explicit Equation for Friction Factor."Flow of Fluids Through Valves, Fittings, and Pipe," Crane Technical Paper 410-C.
Taggart, R.C., and L.E. Cayanus. On-Line Analyzer Sample Conditioning Systems - 'A Guide for Sizing Sample Lines and Flow Indicators.' ABB Process Analytics.





